Eigenmodes of Brain Activity

Eigenmodes of Brain Activity refers to a young paradigm within neuroscience, first proposed by Selen Atasoy, Isaac Donnelly, and Joel Pearson in 2016. It has been included in the QRI lineages due to its elegance and close connection to subjective states.

The core idea is to treat the human brain not as a collection of independent processing units but as a dynamic system whose behavior is constrained by its physical structure. When a neuron gets excited, this excitation spreads to neighboring neurons, leading to a propagation of activity throughout the brain tissue. Using mathematical modeling, it is possible to compute the eigenmodes of this process. Roughly put, these are the modes of activity that "come naturally" to the brain. Empirical results show that brain activity can be approximated by a weighted sum of these modes, even if only a limited set of modes is considered.

In the original formulation by Selen Atasoy et al., the calculations were based on a map of the human connectome, leading to the name Connectome-Specific Harmonic Waves (CSHW). However, a more recent paper by James C. Pang, Kevin M. Aquino, et al. found that computing the eigenmodes based solely on brain geometry yields both stronger results and a simpler model. Since these improved eigenmodes are no longer connectome-specific, the original name has become obsolete.

Layman Explanation

When a guitar string is repeatedly plucked, it will produce a similar note each time. This note will sound different from the one a different instrument would produce, like a harp, even if both strings play at the same pitch. (The set of qualities that can differ among two notes with identical pitch is called timbre.)

However, the sounds humans perceive are based entirely on the vibrations transmitted through the air, which in turn depend almost entirely on how the string vibrates. Consequently, it must be possible to make a guitar string sound like a harp – in fact, it must be possible to produce any sound, regardless of timbre or pitch. Given this physical fact, why is it that we use different instruments, and different strings or keys on one instrument? Why can guitar players not control the timbre of their sound so as to make other instruments redundant?

The answer is that each string has a particular way that it "wants" to vibrate. When the string is perturbed, the vibration is chaotic at first, but it tends to morph into a certain kind of note, usually so quickly that most people perceive it as instantaneous. The reasons for this process are complex, but the bottom line is that making a string do anything other than what it wants is extremely difficult. This "preference" of the string is not absolute – different plucking techniques can have an audible effect on the note – but it is powerful enough that plucking a string almost always gives away the instrument.

Since a guitar has several strings, it can be viewed as a system that likes a small set of sounds. Note that this includes not only the notes each string can produce individually but also the full set of sounds that result from combining the notes of different strings.

The core claim of the "Eigenmodes paradigm" is that patterns of activity produced by the human brain have major similarities to notes played by a guitar. Just like a guitar can, in principle, produce arbitrary sounds, our brain can, in principle, produce arbitrary patterns of activity, but there seems to be a set of patterns it prefers over others. These patterns are called its eigenmodes, and the brain's overall activity can be analyzed in terms of those modes. It seems that our brains almost never "play" at only a single mode, but considering a small set (e.g., the most important 10) tends to account for a sizeable portion of its activity. The significance of these eigenmodes and their precise computational role is a topic of ongoing research.

Finally, note that this analogy reflects genuine mathematical commonalities. While the kind of oscillation is very different – each part of a string vibrates up and down by converting potential to kinetic energy and back, whereas the brain "oscillates" by moving electrical charge around – the resulting motions can be described using the same class of models. These models come from the branch of physics that studies coupled oscillators.

Technical Explanation

Eigenmodes in Periodic Systems

Three animations showing three modes of behavior for a system of two coupled pendulums. The second and third animations depict the two eigenmodes of the system, whereas the first depicts a non-eigenmode. Note that when the gif resets, all three animations start from their initial positions described in the text. (If the animation doesn't play, click here to open it in a separate window.)

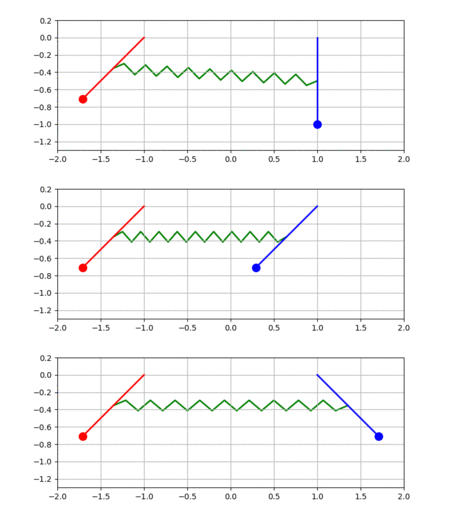
Consider a system of components that can each vary within a fixed range of values, with connections between those components enabling mutual interaction. Our running example will be two pendulums connected by a spring – each pendulum can swing back and forth within a specific range, and the spring allows them to pull and push on each other. If each component undergoes a simple periodic motion (i.e., it repeats its movement over and over again) and the time per repetition is the same for each, then the system is said to be in an eigenmode, and the time per repetition is called their common period. Typically, eigenmodes are special cases among a vast set of behaviors that do not have these properties.

If there are no external influences on the system, then the behavior of each component is determined entirely by its initial position. In our example, we will only consider differences in the pendulums' initial displacement from their resting state. Since eigenmodes are rare, almost all such displacements will result in a pattern of motion that is not an eigenmode. One such example is shown in the first animation to the right. Here, the red pendulum starts off pulled to the left, and the blue pendulum starts off in its resting position in the middle. You can see how the blue pendulum moves slowly at first but accelerates over time, whereas the red pendulum does the opposite, until eventually they switch. The maximum displacement reached by either pendulum throughout this process is identical to the initial displacement of the red pendulum.

There are exactly two eigenmodes of this system, which are depicted in the second and third animations to the right. In the first eigenmode, both pendulums start off pulled the same distance from their resting state in the same direction. In the second eigenmode, the pendulums also start off pulled the same distance from their resting state but in opposite directions. In either case, both pendulums repeat the same motion over and over again, and the period for both pendulums is identical. However, note that the period is only the same for both pendulums within the same eigenmode, not for pendulums in different eigenmodes. In fact, the period in the second eigenmode is slightly smaller than in the first because the spring between the pendulums accelerates their motion. This is why the animations start off in sync but slowly desynchronize over time.

These systems are known as coupled oscillators. Here, the word "oscillator" refers to any object that can undergo periodic motion, and the coupling indicates a causal link between them, such as the spring in our example.

An elementary result of this field is that any system of $N$ coupled oscillators has at most (and usually exactly) $N$ eigenmodes. In our example, there are two coupled pendulums and hence two eigenmodes. Another result is that any pattern of behavior can be written as a weighted sum of the system's eigenmodes. In our case, the motion depicted in the first animation is equal to $0.5$ times the first eigenmode plus $0.5$ times the second. Concretely, this means that at every point in time, the angle of the red pendulum in the first animation is precisely equal to the average of its two angles in the second and third animation. This relationship explains why, whenever the red pendulum swings in opposite directions in the second and third animation, it only exhibits a slight movement in the first animation (the average of a positive and negative angle is about zero), whereas whenever they are in sync, the red pendulum in the first animation swings similarly wide into the same direction (the average of two similar angles is itself similar to each). Naturally, the analogous relationship holds for the blue pendulum.

Other patterns may have different weights, which can also be negative. For example, there exists a pattern that equals $1.4$ times the first eigenmode minus $0.4$ times the second. But every pattern can be written as a weighted sum of eigenmodes, regardless of its complexity.

In practice, these pendulums would gradually slow down over time due to air resistance. This effect is called damping and can also be modeled but at the cost of making the calculations more complex. Finally, note that eigenmodes can also be defined for systems that don't exhibit periodic behavior, but only periodic systems are relevant for this article. Eigenmodes in periodic systems are also called normal modes.

Eigenmodes in a String

An animation showing the first four eigenmodes (or harmonics) of a vibrating string. (If the animation doesn't play, click here to open it in a separate window.)

In a vibrating string, both the spatial arrangement of the string, and the temporal movement of each part of the string are described by the sine function. In the first case, both axes are spatial, so the sine wave simply depicts a string at a point in time (in fact, the animation was created by plotting different sine functions across time). In the second case, the x-axis denotes time and the y-axis vertical oscillation. Thus, the shape of the function shows that each part of the string moves most quickly near its resting state and most slowly at the points of maximum displacement (either upward or downward), where the function is almost flat.

For a vibrating string, each point is considered its own oscillator, where the oscillation is a vertical movement up and down. Thus, the entire string is modeled as a continuous array of coupled oscillators. Despite this change from two oscillators to infinitely many, the results about oscillators discussed in the previous section still apply. In fact, it's not unusual in mathematics to extend discrete models to continuous ones, and properties of the model tend to survive this extension remarkably often.

The first four eigenmodes of the string are depicted to the right. All other eigenmodes follow the same pattern, with each successive eigenmode having one more peak or valley than the one before. Consequently, the period in the $n$-th eigenmode (remember that all oscillators within one eigenmode share a common period) is exactly ${\frac {1}{n}}$-th as large as the period in the first.

For a string and other musical instruments, the eigenmodes are also called harmonics. Any idealized string has infinitely many harmonics (because it consists of infinitely many oscillators), but it's usually sufficient to consider a finite subset.

While the definition of eigenmode is still temporal – each oscillator must have the same period – you can see that the eigenmodes now also exhibit a wave-like pattern through space. This connection between the temporal and spatial patterns is expressed by a famous physical law called the wave equation:

$${\frac {\partial ^{2}u}{\partial t^{2}}}=c^{2}{\frac {\partial ^{2}u}{\partial x^{2}}}$$

Here, $u$ denotes displacement in the direction of vibration (in our case, vertical), $t$ denotes time, $x$ denotes the direction of the wave (in our case, horizontal), and $c$ is a constant. Thus, the wave equation states that for any continuous system of coupled oscillators, the second derivative of the displacement in time is proportional to the second derivative of the displacement in space. Note that the second derivative of a sine function is itself a sine function, so in simple cases, proportionality also holds for the displacements themselves.

When a real string is plucked, its vibration is initially chaotic, but the first harmonic/eigenmode tends to become dominant over time, and analogous behaviors can be observed for other systems of coupled oscillators. This tendency of physical systems to "pick out" or "self-organize around" a particular frequency is not only foundational to the paradigm of cortical eigenmodes, but also to the physical mechanisms underlying sound and music, and indeed to many other processes in nature. In fact, everything in this article up to this paragraph has been entirely about mathematical modeling. If eigenmodes did not occur naturally in real systems, the utility of such models would be vastly diminished.

The mechanisms that cause this tendency are multi-faceted, but one of the most important ones is that the rate at which a particle loses energy is correlated with its velocity – and as you can verify in the animations on the right, the first harmonic is the "slowest", having the least mean velocity of particles across the string body. Recall that any behavior can be written as a weighted sum of eigenmodes, so if the higher harmonics of a string fade, the first harmonic is the only component that remains. In a real string, this principle almost always holds even though all of the harmonics act on the same string simultaneously, which means that the velocity of any one particle is the sum of many (often mutually opposing) components.

Eigenmodes in the Brain

To compute the eigenmodes of the brain, the surface of the neocortex is modeled as a continuous array of coupled oscillators. In this way, the model is similar to a guitar string, except that there are two spatial dimensions instead of one. However, the mode of oscillation is different: instead of a spatial vibration, the points on the surface can cycle through varying levels of activity.

In both of the two major papers that have been published about the paradigm, the eigenmodes have been computed based entirely on the spatial dimension. (For some tasks where the temporal axis is important, several such eigenmodes corresponding to different points in time have been combined, but details are omitted here.) Thus, each eigenmode is a distribution of activity across the cortical surface, which can be considered analogous to a snapshot of a vibrating string at a single point in time. Due to the relation expressed by the wave equation, it is reasonable to expect the existence of temporal patterns that correspond to these spatial patterns.

If the brain's surface were perfectly smooth, the eigenmodes might have a very simple shape, like a sinusoidal curve in two dimensions. In practice, the irregular shape of the cortex affects the propagation of activity (and hence the shape of eigenmodes), which makes the actual eigenmodes too complicated to write down fully. However, they are still approximately sinusoidal.

To empirically validate the approach, a number of snapshots of brain activity have been taken and compared to a reconstruction based on a weighted sum of eigenmodes. Since any pattern of activity can be written as a weighted sum of eigenmodes, the fact that such a sum can approximate brain activity is trivial, but the number of modes required for the approximation is not. If the brain's eigenmodes were purely mathematical artifacts with no biological significance, we might expect it to take a large number of eigenmodes to approximate any given distribution of activity. Instead, it's been shown that a much smaller number yields nontrivial results, with the modes that have the lowest spatial frequency consistently playing the largest role. See the Results section for details.

Resonance

Resonance refers to the process by which an external force is applied to an oscillator in such a way that it strengthens the movement that the oscillator already exhibits. Such a force can counteract damping and thus maintain an oscillation across time. For example, when children play on a swing set, they will typically time their efforts to match the motion that the swing already exhibits. Conversely, if you tried to accelerate a swing set with deliberately miss-timed movements, the force you applied would not be in resonance with the existing oscillation, and its effectiveness would be greatly reduced.

Technical Footnotes

• The definition of eigenmode given above is not precise. The proper definition includes the concept of phase, specifically the relative phase between two oscillators. The problem with the definition used here is that it relies on the concept of a "simple periodic motion", which is not well-defined. In particular, one could define the blue pendulum's motion in the first animation as spanning the full time from its initial resting state to when it eventually slows down again (and analogously for the red pendulum). Under this definition, the motion would, in fact, be periodic, and both pendulums would even share the same period. However, the period would be very large since each motion would include many oscillations around the resting state. This complication is why non-eigenmodes have been described as "complex" rather than "aperiodic".
• The claim that the system has two eigenmodes is a simplification. The more precise statement is that the system has two classes of eigenmodes, with each class consisting of an infinite family of different eigenmodes with varying amplitude. E.g., both pendulums may be moved 1cm, 2cm, or any other amount to the left, and each choice will lead to a mode in the first family of eigenmodes, with the only difference being the amplitude of the oscillation. The period of the eigenmode is independent of the initial displacement, although this fact relies on simplifying assumptions like the absence of air resistance.
• A particularly important simplifying assumption is called the small-angle approximation. When our example system of two coupled pendulums is properly analyzed using a force diagram and applying Newton's second law of motion, one derives a pair of differential equations that describe the movement of each pendulum as a function of time. These equations include the terms $sin(\theta )$ and $cos(\theta )$, where $\theta$ is the angle of oscillation. If these terms are included, the equations do not have a closed-form solution, and they are also non-linear, which means that writing movement patterns as weighted sums of eigenmodes is no longer possible. To make the problem easier, one generally assumes that $\sin(\theta )=\theta$ and $\cos(\theta )=1$, which is approximately true if $\theta$ is small (hence the name "small angle approximation"). The upshot is that the behavior predicted by simplified mathematical models tends to become increasingly inaccurate as the amplitude of oscillation grows, which has important consequences in many practical cases. A related concept is the Superposition Principle, which applies to coupled oscillators only if the equations are linear.

Results

A graphic summarizing empirical results of the eigenmodes paradigm. See the text for details.

Empirical results show that a relatively small number of modes is enough to approximate cortical activity with a reasonable level of accuracy:

We observe that reconstruction accuracy increases with an increasing number of modes across all task contrasts and in the resting state, with r ≥ 0.38 already achieved using just N = 10 modes (Fig. 1d). Large-scale modes are also differentially recruited across different tasks, suggesting that particular stimuli excite specific modes (Fig. 1e). Improvements in reconstruction accuracy become slow after ten modes, reaching r ≥ 0.80 at approximately N = 100 modes, with only incremental increases in reconstruction accuracy beyond this point. Because the first 100 modes have wavelengths above around 40 mm (Supplementary Table 1), and the inclusion of shorter-wavelength modes only refines the reconstruction of localized patterns (arrowheads in Fig. 1e), our findings suggest that the data are predominantly comprised of spatial patterns with long spatial wavelengths (see next section for a more detailed analysis).

(From Geometric Constraints on Human Brain Function, p. 2.) To the right, you can see a (slightly cropped) version of Figure 1 from the paper. Here,

• (a) shows a visualization of the first few eigenmodes as heat maps, with red and blue denoting high and low levels of activity, respectively. Note that the first eigenmode (unlike all others) has a wavelength much larger than the human brain. It is effectively a constant function that adds the same amount of activity to every point on the cortex.
• (b) shows a graphical illustration of how a weighted sum of modes can approximate an activity distribution.
• (c) shows how "spontaneous" activities with an important temporal component are approximated by sequential reconstructions for different points in time.
• (d) shows a plot of reconstruction accuracy as a function of the number of modes considered (with separate graphs for separate tasks).
• (e) shows sample heat maps for various brain activities (left column), as well as heat maps from reconstructions based on the first 10, 50, and 200 eigenmodes (right column).

It's worth pointing out that "brain activity" in this context actually refers to blood flow through the brain. This is so not because blood flow is the more important target but because it is much easier to measure. Such blood flow is a reliable but noisy proxy for electrical activity. Reconstruction accuracy would likely be improved if both the data and eigenmodes were based directly on the distribution of electrical charge, but the amount of improvement is unclear.

Besides the neocortex, a variant of the method using a 3-dimensional model has also been applied to the thalamus, striatum, and hippocampus (p. 6f in the paper). Note that the neocortex is by far the largest brain area, comprising around three-quarters of its total volume.

Significance

In 2018, QRI co-founder Michael Edward Johnson wrote a post about the paradigm (which at the time was still known as Connectome-Specific Harmonic Waves, CSHW) that primarily discusses its potential. This section will provide a brief summary, but readers are encouraged to read the full piece.

1. If the Symmetry Theory of Valence is true, the distribution of eigenmodes is likely to be a major contributing factor to the valence of the conscious state exhibited by the brain. This is because different eigenmodes can be mutually consonant (and hence symmetrical) or dissonant, just like different notes of a piano can form a consonant or dissonant chord.
2. Eigenmodes might provide the tools for an improved measure of intelligence. E.g., a major correlate of observed intelligence might be the ability to navigate between different modes.
3. Interpersonal connection could be analyzed in terms of the eigenmodes of the people involved. Relatedly, Emotional Intelligence (EQ) might cash out as the ability to simulate another person's eigenmodes.
4. Language processing in the brain could be analyzed by modeling different words as pointers to different modes or combinations of modes.
5. Culture wars and societal conflict might be understood as different memeplexes that activate mutually dissonant sets of eigenmodes.

Furthermore, QRI president and co-founder Andrés Gómez Emilsson has indicated that the brain's eigenmodes may play a crucial role in solving the Boundary Problem.

Note that because of Dual-Aspect Monism, every phenomenological or philosophical role of the brain's eigenmodes must have a corresponding computational aspect. For example, if the consonance or dissonance between different modes is related to valence, then there must be a corresponding physical mechanism that causes the behavior humans exhibit in response to high or low valence. A likely candidate here would be a tendency of the brain to optimize for consonant arrangements, corresponding to people's tendency to seek out high valence states.

As of today, most of these ideas remain speculative, but there has been some empirical work, including a follow-up paper by Selen Atasoy et al. examining the effect of LSD on the brain's eigenmodes.

Resources

• Geometric Constraints on Human Brain Function – the paper that introduced improved (geometric) eigenmodes. It's freely accessible at Nature and relatively readable.
• ActInf GuestStream 055.1~ James Pang & Alex Fornito "Geometric constraints on human brain function" – a presentation about the paper by its two primary authors.
• Human brain networks function in connectome-specific harmonic waves – the original paper that spear-headed the paradigm. It's also freely accessible at Nature but highly technical.
• A Future for Neuroscience – a blog post about the paradigm by QRI co-founder Micheal Edward Johneson. Note that this post was written when the paradigm was still known as "Connectome-Specific Harmonic Waves" (CSHW).
• Connectome-harmonic decomposition of human brain activity reveals dynamical repertoire re-organization under LSD – a follow-up paper by Selen Atasoy et al. that applies the paradigm to data collected from patients under the effects of LSD, also freely accessible at Nature.
• Selen Atasoy: Enhanced Improvisation in LSD Brain Processing – a YouTube video of a talk related to the above paper.
• Human brain networks function in connectome-specific harmonic waves: Derivative Papers – a list of academic papers that cite the CSHW paper, generated by the "Connected Papers" website.
• On Connectome and Geometric Eigenmodes of Brain Activity – an introductory video published on the QRI YouTube channel.