Symmetry Theory of Valence
The Symmetry Theory of Valence (STV) is the hypothesis that the valence of a moment of consciousness is precisely determined by the symmetry of the mathematical object that describes it. The STV was proposed by QRI co-founder Michael Edward Johnson in his short book PrincipiaQualia in 2016.[1]
Layman Explanation
We often talk as if some activities are inherently pleasant or unpleasant, but this can't quite be true. Consider:
- combining several activities can be more or less fun than the sum of their parts – listening to a catchy song while working on a complex problem may not go well together, even if each one would have been enjoyable by itself.
- how good an activity feels depends on your mood – lying on the beach may not be so pleasant if you feel restless and driven.
- during meditation, one may experience high levels of fulfillment by simply observing the breath.
What is the alternative? Observe that consciousness appears to be inherently spatial: we continuously perceive a three-dimensional expanse, and different qualia appear at different places in this "phenomenal space". You can liken your consciousness to a large canvas on which the brain "paints" qualia to represent both sensory inputs and thoughts. In this view, pleasantness is a global property of the entire painting. That means pleasantness is influenced by content because certain inputs tend to be represented by certain qualia, but it is only an approximation since several other factors can contribute to the painting's global structure. Most importantly, it depends on how different qualia fit, both with each other (see also consciousness as a musical instrument) and with what's called the "noise signature" of consciousness, which is a global property that gives rise to your current mood. In the painting analogy, you can think of it as the background or color palette.
It is also possible to change the nature of qualia without changing their content. For example, paying attention to a single stimulus over a long period will tend to make it stronger and more detailed. There is also a meditative technique called equanimity that can be applied to arbitrary sensations, which tends to make them less painful (if they're negative) or more fulfilling (if they're positive), again without changing their content. In the painting analogy, these techniques are like drawing the same thing with a different art style.
Building on this framework, the Symmetry Theory of Valence (STV) says that the structural property that counts is the symmetry of the painting. Here, the term valence is a catch-all for all positive (and negative) sensations, subsuming happiness, pleasure, love, contentment, intellectual satisfaction, and any other flavor of well-being. A large chunk of what motivates the STV depends on technical details of how qualia are physically instantiated, but it also has aspects that can be appreciated from direct observation. Most notably, it explains why we like symmetry in sensory inputs (since symmetrical inputs tend to lead to symmetrical qualia), such as in symmetrical faces or architectures. If you are indoors right now, you can probably find deliberate symmetry in almost every object in your environment. Note also that harmony in music exhibits symmetry across time on the physical level.
Technical Explanation
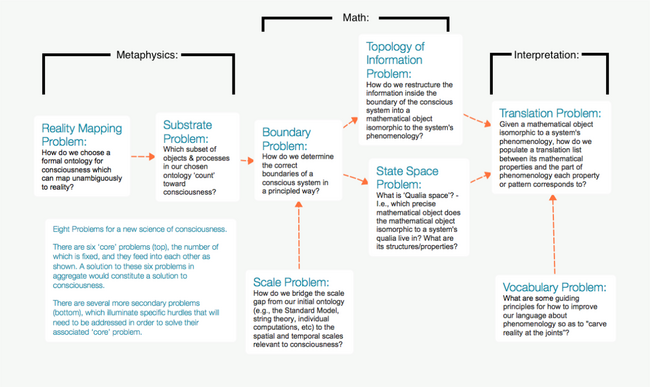
Prior Concepts
The STV relies on several assumptions about the nature of consciousness, which are briefly listed here (see also the list of subproblems on the right):
- Consciousness Realism: consciousness is a fundamental and frame-invariant aspect of the universe, not a leaky abstraction.
- Physicalism: the laws of physics exhaustively describe the causal behavior of every feature of the universe, including consciousness.
- Qualia Formalism: consciousness is quantitative; it can be described precisely by a mathematical object.
- Qualia Structuralism: this object has regularity and structure.
Stating the Thesis
The STV states that the valence of a moment of consciousness corresponds to the symmetry in its mathematical object.
It's important to note that the STV is not meant to be a heuristic or specific to human brains, but a law of nature that applies precisely and universally, to all conscious systems and without exception.
Formalization
Suppose is the set of all possible sequences of whatever neuroimaging data is used to analyze a brain. Then, the State-Space Problem can be formalized as finding a set that's the space of all possible moments of consciousness, the Topology of Information Problem as finding a function that transforms a concrete set of neuroimaging data into an object from this space, and the Interpretation Problem as finding an "interpreter" that extracts all properties of interest from the object . In this setting, the STV is the claim that the valence values reported by correspond to the symmetry in . Taken together, the pair both constructs and interprets the mathematical object, thereby constituting a complete solution to consciousness.
Conversely, the three prior problems (Reality Mapping-, Substrate-, and Boundary Problem) are all necessary prerequisites to defining this pair. E.g., a solution to the substrate problem is required to know which neuroimaging data to use and how to interpret it.
It's worth noting that the choice of is not arbitrary. (If it were, the STV would be ill-defined since for any pair , there are infinitely many other pairs yielding the same interpretation utilizing different mathematical objects.) Mike Johnson suggested that the choice may eventually become trivial,[2] i.e., once one has identified the correct ontology, the correct physical substrate, and the proper boundaries around the substrate, the object may become synonymous with the physical description of the substrate, with no further transformation needed. Short of that, one may still privilege constructions that keep the transformations as small as possible (note that this can be formalized by the minimum description length of ). In either case, it is unlikely that the amount of symmetry would be dramatically different between plausible candidate objects. Applications of the STV usually assume that intuitively important properties are preserved so that, e.g., symmetry in sensory input like music leads to symmetry in the object .
Resources
- The Symmetry Theory of Valence 2020 Overview – a summary on work about the STV by Andrés.
- A Primer on the Symmetry Theory of Valence – a blog post on the STV by Mike Johnson.
- The Symmetry Theory of Valence (@The Centre for Psychedelic Research at Imperial College London) – a presentation by Andrés.
- The Symmetries of the universe – a video about symmetries in the standard model of physics on the ScienceClic English channel.
References
- ↑ Johnson, M. E. (2016). Principia Qualia. Retrieved from https://opentheory.net/2016/11/principia-qualia
- ↑ Johnson, M. E. (2024). Private Conversation.








